Forsendur t-prˇfs:
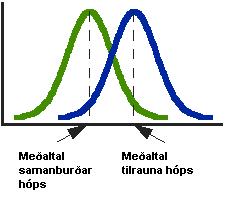
Mynd 1. DŠmi um dreifingu tveggja hˇpa a lokinni tilraun.
Ůegar liti er ß mynd 1. sřnir h˙n dreifingu tveggja ˙rtaka, samanburarhˇps og tilraunahˇps Ý rannsˇkn. Myndin sřnir jafna dreifingu Ý hˇpunum. Dreifingin er yfirleitt sřnd me s˙luriti, st÷plariti ea lÝnuriti. Myndin segir okkur frß hvernig dreifingin er Ý ˙rtakinu. T-prˇfunin svarar spurningum um hvort a mealt÷l ˙rtakana eru me t÷lfrŠilega martŠkan mun.
Til a athuga betur hva ßtt er vi me marktŠkum mun skulum vi lÝta ß ■rjßr ˇlÝkar rannsˇknar niurst÷ur sem sřndar eru ß mynd 2. Ůa fyrsta sem vi t÷kum eftir er a Ý ÷llum niurst÷unum er munurinn ß mealt÷lunum sß sami en gr÷fin lÝta ekki eins ˙t, og ■ar me segja ■au mj÷g ˇlÝka s÷gu. ┴ efstu myndinni sjßum vi milungs dreifinu Ý hˇpunum. ┴ annarri myndinni sjßum vi mikla dreifingu Ý hˇpunum en ß ■riju myndinni er dreifingin mj÷g lÝtil. Ůar sem dreifing hˇpana Ý nestu myndinni er mj÷g lÝtil ■ß skarast ■eir lÝti. En ß mynd tv÷ er mikil sk÷run ■annig a vi getum gefi okkur a hˇparnir eigi margt sameiginlegt.
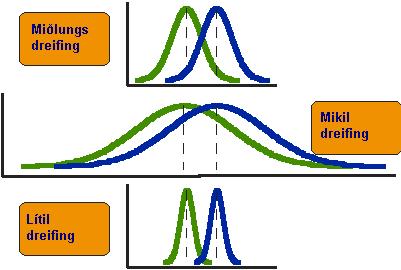
Mynd 2. Ůrj˙ dŠmi um mismundandi dreifingu hˇpa.
Ůegar vi erum a horfa ß muninn ß milli tveggja ˙rtaka ■ß verum vi a meta muninn ß mealt÷lunum Ý tengslum vi dreifingu gildana Ý hverju ˙rtaki. Ůetta er nßkvŠmlega ■a sem t-prˇfi gerir.
Para t-prˇf (paired samples test) byggist ß ■vÝ a nota mismunat÷lur. ═ sta tveggja hßra mŠling er notu ein mismunatala fyrir hvert par ľ sem samanstendur af tveimur hˇpum. Ůannig er fyrri mŠlingin dregin frß ■eirri seinni og niurst÷urnar eru prˇfaar me t-prˇfi. Ef enginn munur er ß fyrri og seinni prˇfun Štti mismunur hˇpanna a vera 0,0, en ■a mß prˇfa me einshˇps t-prˇfi. T÷kum mismunat÷luna, reiknum staalfrßvik, staalvillu og framkvŠmum t-prˇf.
Form˙lan fyrir t-prˇfi er hlutfall. ═ nefnara er hlutfalli ß muninum milli mealtalna (mismunatala) en Ý teljara er metin dreifing gildanna Ý hverjum hˇpi (staalfrßvik). Ůessi form˙la segir okkur muninn ß tilraunahˇpnum og samanburarhˇpnum og einnig hve mikil dreifing er innan hˇpanna. Dreifing innan hˇpanna er mikilvŠg til a greina muninn ß milli ˙rtakanna. Mynd 3. gefur okkur form˙luna fyrir t-prˇfun og hvernig nefnarinn og teljarinn eru tengdir dreifingu innan hˇpana.
Setja inn ori staalvilla Ý sta Dreifing hˇpanna
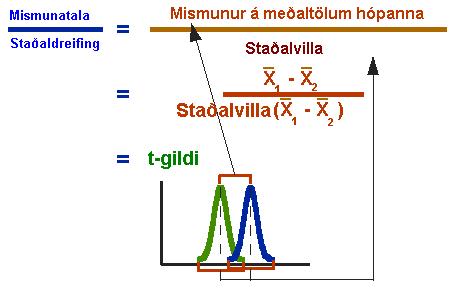
Mynd 3. t-prˇfs form˙lan.
Ůa er auvelt a reikna ˙t nefnarann, ■.e. muninn (mismunat÷luna) ß milli mealtalna hˇpanna og ˙tkoma ˙t ˙r teljaranum er kallaur staalvilla mismunanna (standard error of the difference). Til a reikna teljarann ■ß t÷kum vi dreifingu (variance) hvers hˇps og deilum Ý me fj÷lda innan hvers hˇps. SÝan leggjum vi ■essi tv÷ gildi saman og t÷kum kvaratrˇtina af ■eirri t÷lu (sjß mynd 4).
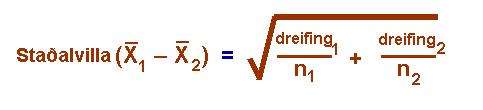
Mynd 4. Form˙la fyrir staaldreifingu.
┴ mynd 5 mß sjß endalega form˙lu fyrir t-prˇfi.

Mynd 5. Form˙la fyrir t-test.
Niurstaa T-prˇfs verur jßkvŠtt ef fyrra mealtali er stŠrra en ■a seinna, en neikvŠtt ef seinna mealtali er stŠrra en ■a fyrra. Ůegar ■˙ er komin me ˙tkomu ß t-prˇfinu ■ß ■arf a leita upp Ý t÷flum til a athuga marktekt prˇfsins, er hlutfalli nˇgu stˇrt til a hŠgt sÚ a segja a niurst÷ur tilraunarinnar er ekki eing÷ngu komin til vegna tilviljunar. Til a meta markteknina ■ß er nausynlegt a velja ÷ryggism÷rk (alpha level). ═ flestum rannsˇknum sem gerar eru Ý fÚlagsvÝsindum ■ß er sett ■umalfingurregla um a marktektin sÚ vi 0,05. Ůetta ■řir a Ý fimm skiptum af hundra ■ß kemur ˙t marktekur munur ß mealt÷lunum jafnvel ■ˇ a ekki sÚ um marktekni a rŠa ea ■a kemur fram af tilviljun. Ů˙ verur einnig a ßkvea frÝgrßu (df, degrees of freedom) fyrir prˇfi. Ůegar gert er t-prˇf ■ß er frÝgrßan (df) heildarfj÷ldi staka Ý hverjum hˇp mÝnus 2. Ůegar ■˙ hefur nß Ý ÷ryggism÷rkin (alpha level), frÝgrßuna og t-gildi, ■ß getur ■˙ flett upp hvort a prˇfi er marktekt og meti hvort a t-gildi er nˇgu stˇrt til a vera marktekt. Ef prˇfi er marktekt ■ß getur ■˙ ßlykta svo a munurinn ß milli mealtalna hˇpanna sÚ ■a mikill a jafnvel liti til breytileikans ■ß sÚ munurinn til staar.
T-prˇfi er ■eim kostum b˙i a ■a er s˙ afer vi prˇfun tilgßtunnar sem er lang afkastamest, miklu afkastameira en alsherjarprˇf. Tilgßtan sem sett er fram Ý upphafi rannsˇknar er skřr og gefur skřra lřsingu ß ■eim niurst÷um sem vŠnst er sem er prˇfu me miklum afk÷stum.
© 2003 Sig■r˙ur Erla Arnardˇttir