Úrtakadreifing (sampling distribution) er dreifing mælitalna milli úrtaka. Það byggir á mismunandi einstaklingum sem veljast í úrtökin, þannig verða úrtökin ólík og hversu ólík þau verða er háð stærð úrtaksins. Því minna sem úrtökin eru því ólíkari verða þau hvert öðru. Úrtakið er breytilegt eftir stærð þannig að meðaltal meðaltalnanna er svipað, óháð úrtaksstærð en staðlfrávikið minnkar með stærra úrtaki. Því stærra sem úrtakið er þeim mun líkara er það öllu þýðinu og ef við værum að gera athugun og notuðum ekki úrtak heldu athugun á öllu þýðinu þá væri ekkert staðalfrávik þar sem við værum ekki með úrtak. Ef mjög mörg tilviljunarúrtök eru dregin úr þýði verður úrtakadreifing meðaltalnanna mjög nálægt því að vera normal, eins og hún er í þýðinu. En hér veltur á að úrtaksstærðin sé stór.

Við þekkjum eiginleika þýðis og viljum vita hvernig eiginleikar úrtaksins muni dreifast og þá reiknum við út öryggisbilið. Til þess að reikna út öryggisbilið þurfum við að vera búin að reikna út staðalvillu meðaltalanna. Við ályktum um þýðið út frá úrtakinu

Úrtaksmeðaltöl er normaldreifð með miðju á m og staðalvillu (staðalfrávik meðaltala). Staðalfrávik segir okkur hvernig ákveðin svörun er dreifð í kringum meðaltalið en staðalvilla segir okkur dreifingu í kringum meðaltal í úrtakinu. Öryggismörk er lýsing á því á hvaða bili úrtaksmeðaltalið er líklegt til að dreifast. Lítum á mynd 1.

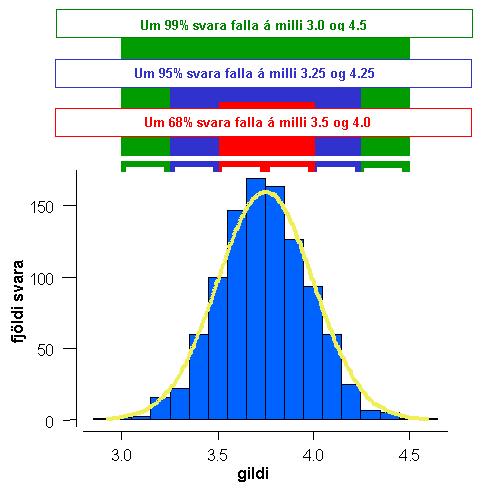
Mynd 1. Öryggismörk.

Við erum með normaldreifingu í þýðinu og fáum einnig normal dreifingu í úrtakinu þar sem við lögðum áherslu á að hafa úrtakið eins stórt og nauðsynlegt var til að fá lýsandi úrtak úr þýðinu. Þegar litið er á meðaltalið þá eru flestir sem lenda í miðjunni eða um 68% hópsins (rautt). Þannig að ef við förum upp um eitt staðalfrávik eða niður um eitt staðalfrávik þá erum við með 68% af úrtakinu í þeim hópi. Ef við förum upp eða niður um tvö staðalfrávik þá erum við komin með 95% af hópnum (blátt). En þrjú staðalfrávik upp eða niður gefa okkur 99% af hópnum (grænt). Þessi regla gildi alveg sama hvort verið er að tala um staðalfrávik eða staðalvillu. Algengast er að miða við 95% öryggi en þá falla 5% úrtaksmeðaltalanna utan bilsins sem er táknað með a = 0,05. Þessi 5% skiptast í tvo helminga fyrir ofan bilið og fyrir neðan, 2,5% eru fyrir ofan og 2,5% eru fyrir neðan.

Nú þegar við getum metið úrtakið okkar þá er mikilvægt að meta það út frá því hvernig það svarar miðað við þýðið í heild sinni. Því tökum við staðalvilluna og reiknum út öryggisbilið og fáum þá upplýsingar um hvernig það svaraði í hlutfalli við allt þýðið. Tökum dæmi til að útskýra þetta betur (sjá mynd 2).

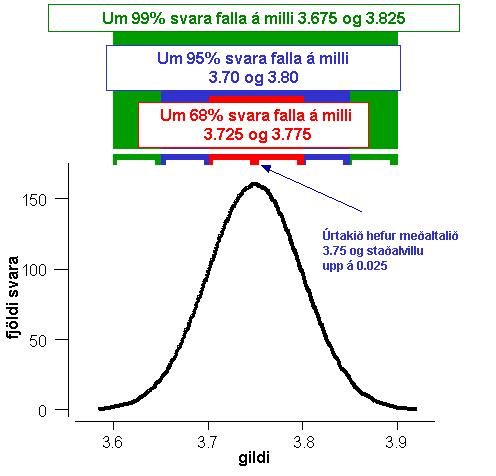
Mynd 2. Öryggisbil.

Í þessu dæmi er meðaltal hópsins 3,75 og staðalfrávikið er 0,25. Við getum út frá þessum upplýsingu metið úrtakið og á hvaða bili hópurinn er líklegur til að svara út frá 68%, 95% og 99% öryggismörkum. Þannig reiknum við öryggisbilið með því að taka meðaltalið og leggja við og draga frá staðalvilluna (sjá mynd 2).

© 2003 Sigþrúður Erla Arnardóttir