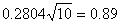
Hægt er að reikna φ ef búið er að reikna φ' en það er gert á eftirfarandi hátt.

Athugið að hér er ekki átt við fylgnistuðulinn φ. Þó í báðum tilfellum sé talað um fí, er um ólíkar stærðir að ræða.

Áhrifastærðin þarf að vera fyrir hendi við útreikningana en auk hennar þarf einnig að liggja fyrir fjöldinn í hverju hólfi.

Hægt er að nota aðra af eftirfarandi formúlum til að reikna áhrifastærð og fjölda í hverju hólfi saman í mælitöluna φ.

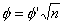
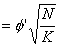
Þegar φ'er reiknað þá þarf ekki að taka n með í reikninginn. Hins vegar er n tekið með í reikninginn þegar φ er reiknað. Hægt er að nota niðurstöður φ til að fletta upp í töflunni noncentral F distribution, til þess að fá upplýsingar um afköstin. Töfluna er meðal annars að finna á blaðsíðu 740 í bókinni Statistical Methods for Psychology eftir D.C. Howell. (2002). Auk φ þá þarf einnig að hafa frígráðurnar og frígráður villunnar fyrir hendi svo hægt sé að finna afköstin.

Vegna þess að við vorum búin að reikna φ' áðan þá getum við notað það til þess að fletta upp afköstunum. φ'= 0.2804 og það voru 10 manns í hverju hólfi.

φ =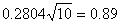

Til að fletta upp í töflunni þá þarf einnig að hafa frígráðurnar, en í rannsókninni voru 5 hópar með 10 manns í hverju hólfi. Frígráðurnar eru 4 og frígráður villunnar 45. Þar af leiðir F (4, 45, 0.89). Þessi tölugildi eru ekki öll fyrir hendi í töflunni, þar sem taflan er ekki mjög nákvæm og því þarf að námunda tölurnar að næstu tölum, við það verða frígráður villunnar = 30 og φ = 1.

Eftirfarandi tölugildi eru því notuð til þess að fletta afköstunum upp; F (4, 30, 1) við það fæst β = 0,66, við alfa = 0,05 úr töflunni.

Afköstin eru reiknuð út á eftirfarandi hátt:

Afköst = 1- β = 1 – 0.66 = 0.33

Þetta eru of lág afköst en við viljum hafa þau 0.80.

Fullnægjandi afköst nást því ekki með 10 manns í hverju hólfi.

Til að finna út hversu marga þátttakendur við þurfum í rannsóknina til þess að ná fullnægjandi afköstum, þá getum við unnið aftur á bak í töflunni.

Við viljum afköst upp á 0.80 en þá er β = 0.20. Nú þurfum við að finna hvað φ er fyrir β = 0.20. Við notum sömu frígráðurnar (4,30) og finnum að næst 0,20 kemst φ = 1.6 sem er 0.24.

Vegna þess að verið er að athuga hversu marga þátttakendur þarf, þá verður formúlan:

n = φ² / φ²’

n = 1.6² / 0.89²

= 32

Þetta þýðir að til þess að ná afköstum upp á um það bil 0,80 þá þurfum við 32 manns í hvert hólf.

φ' minnkar að jafnaði ef mjög ójöfn skipting er í hólfunum. Það leiðir til þess að afköstin minnka, nema að heppnin sé með okkur og ýktustu meðaltölin séu í fjölmennustu hólfunum en við það aukast áhrifin. Hægt er að hámarka áhrif sniðsins með því að ákveða fyrir fram fjölda þátttakenda í hverju hólfi sniðsins.

© 2004 Eva Dögg Gylfadóttir