Formúla fyrir φ'

Áhrifastærð mæld með φ'.

Í töflunni hér að neðan eru meðaltöl, staðalfrávik, dreifitölur og fjöldi í hverju hólfi fyrir árangur ólíkra meðferðarúrræða.

	Meðferð 1	Meðferð 2	Meðferð 3	Meðferð 4	Meðferð 5
Meðaltal	2,22	1,83	2,59	3,76	4,54
Staðalfrávik	3,22	2,38	3,74	3,76	4,54
Dreifitala	10,4	5,7	14,0	14,1	20,6
n	10	10	10	10	10

Hér að neðan er formúla fyrir φ'. Í framhaldi af formúlunni er dæmi um hvernig á að nota hana.

Hægt er að líta á σ_t (fyrir ofan brotalínu) sem óstöðluð áhrif á kvarða fylgibreytunnar.

Þegar við deilum staðalfráviki villunnar sem táknuð er með σ_e (fyrir neðan brotalínu) þá stöðlum við áhrifastærðina, þannig að hægt er að bera saman áhrif ólíkra rannsókna.

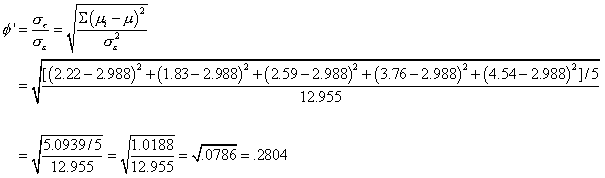Vegna þess að hér er um mörg ólík meðaltöl að ræða, þá þarf að byrja á því að reikna óvegið meðaltal (meðaltal meðaltalanna).

Í þessu tilfelli er óvegna meðaltalið 2.988.

Það er síðan dregið frá meðaltali hvers hóps fyrir sig, eins og sést í dæminu hér að ofan.

Þær útkomur eru hafðar upp í annað veldi, síðan er summa þeirra lögð saman og deilt í þá útkomu með fjölda hópanna.

Hér voru 5 ólík meðferðar úrræði (5 hópar) og því er deilt með 5.

Síðan er deilt í þessa útkomu (1.0188). Talan sem er undir brotalínunni er fengin með því að reikna MSe.

Það er gert með því að leggja saman dreifitölurnar. Dreifitala er staðalfrávikið í öðru veldi.

Síðan er deilt í summu þeirra með fjölda hópanna. 6.477/5 = 12.955

Í þessu tilfelli verður útkoman 12.955.

Loks er svo kvaðratrót tekin af útkomunni, eins og sést í ofangreindu dæmi.

Niðurstaða φ'er = 0,28 sem er rétt yfir miðlungs áhrif.