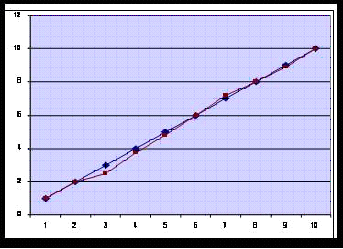
Einn af kostum η² er að hægt er að nota hana til að meta hvort samband tveggja breyta sé línulegt eða í sveiglínu.

Í beinlínutengslum er gert ráð fyrir að áhrif frumbreytu á fylgibreytu séu alltaf þau sömu óháð gildi frumbreytunnar. Beina línan gefur spágildi fyrir fylgibreytuna út frá gildum frumbreytu. Hvernig gildi fylgibreytunnar dreifast í kringum beinu línuna gefur síðan vísbendingar um hversu vel línan lýsir dreifingunni. Með því að setja síðan fylgnina á milli breytanna í annað veldi (r²) fæst skýrð dreifni, hversu mikið frumbreytan skýrir af dreifingu fylgibreytunnar.

Mynd 1. Tengsl breyta sem bein lína lýsir vel. Hér væru η² og r² svipað stór.

Bein lína getur vanmetið styrk tengsla milli breyta (skýrða dreifingu) ef tengslin eru ekki bein, t.d. í sveigboga, því þá er dreifing gilda fylgibreytu mikil í kringum beinu línuna. Það gefur auga leið að ef lína er felld að gildum fylgibreytu gefur hún líklegri spágildi fyrir fylgibreytuna heldur en bein lína. Þá eru frávik fylgibreytunnar mun minni frá línunni. Þetta er einmitt kosturinn við eta. Þegar eta er notað er engin bein lína notuð heldur meðaltal hvers hóps notað sem spágildi fyrir fylgibreytur í þeim hópi. Skýrð dreifing er þá sá hluti af heildardreifingu fylgibreytu sem meðaltöl hópanna ákvarða en ekki beina línan.

Þar sem mælitalan r² er því nokkuð svipað í túlkun og η² er hægt er að nota tengslin milli þeirra til að meta hvort bein lína lýsi tengslunum illa því ef η² er hærra en r² þá lýsir sveiglína tengslunum betur. Ástæðan fyrir þessu er sú r² lýsir hlutfalli dreifingar sem er vegna línulegra tengsla en η² hlutfall dreifingar sem er vegna áhrifa hvers gildis frumbreytu á fylgibreytuna.

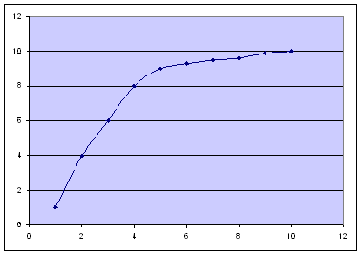
Mynd 2. Tengsl breyta þar sem bein lína lýsir tengslunum illa. Hér myndi η² vera stærra en r² og sveiglína lýsa tengslunum betur en bein lína.

© 2004 Erla Svansdóttir